Fulloriginalsource.com — Alternate interior angles refer to the angles created on opposite sides of a transversal when two parallel lines intersect. In simpler terms, when a transversal intersects two parallel lines, it forms eight angles, and the ones located on the inner side of the parallel lines but on opposite sides of the transversal are termed as alternate interior angles.
alternate interior angles
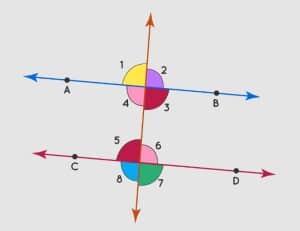
Definition of Alternate Interior Angles:
When a transversal intersects two parallel lines, the pair of angles formed on the inner side of the parallel lines, but on opposite sides of the transversal, is known as alternate interior angles. These angles are always congruent. Additionally, they serve as a criterion for determining whether the intersected lines are parallel; if the alternate interior angles are congruent, the lines are considered parallel.
In the illustration below, AB and CD represent parallel lines intersected by a transversal. According to the alternate interior angles theorem, the pairs of alternate interior are ∠4 and ∠6, as well as ∠3 and ∠5.
Alternate Exterior Angles:
Conversely, alternate exterior angles are angles with different vertices, positioned on alternate sides of the transversal, and are located outside the lines. When a transversal intersects two parallel lines, the alternate exterior angles are always congruent. In the provided figure, ∠1 & ∠7 and ∠2 & ∠8 are examples of pairs of alternate exterior angles.
Converse of the Alternate Interior Angles Theorem:
The converse of the alternate interior angles theorem states that if a transversal intersects two lines in such a way that the alternate interior are congruent, then the two lines are parallel. This is demonstrated in the figure where ∠1 = ∠5 (corresponding angles) and ∠3 = ∠5 (vertically opposite angles), leading to the conclusion that ∠1 = ∠3. Similarly, ∠2 = ∠4, establishing the parallelism of the given lines.
Determining Alternate Interior Angles:

Applying the alternate interior angles theorem, the equality of alternate interior angles in two parallel lines is a fundamental concept. This principle can be used to find these angles, as illustrated in the example involving Sixth Avenue, 1st Street, and 2nd Street. If Maple Avenue is the transversal and the lines are parallel, the measure of angle x can be determined as equal to the given angle of 40°.
Important Notes:
- Each pair of alternate interior angles is congruent.
- Each pair of co-interior angles is supplementary.
- Each pair of corresponding angles is congruent.
- Each pair of alternate exterior angles is congruent.
Challenging Question: In the figure where AB∥CD∥EF, find the value of x.
Topics Related to Alternate Interior Angles:
Explore related topics such as vertical angles, alternate angles, same side interior angles, and an interior angles of polygon calculator for a comprehensive understanding.
Alternate Interior Angles Examples:
Illustrative examples, like those involving finding the measure of angle x, help reinforce the application of the alternate interior theorem.
Practice Questions on Alternate Interior Angles:
Engage in practice questions to further enhance your understanding of alternate interior angle and related concepts.
Q.1. Dolly is asked to determine whether the following statement is True or False. Let’s help her. The angles that lie on the outer side of the parallel lines but on the opposite sides of the transversal are alternate interior angles.
 fulloriginalsource scholarships for college
fulloriginalsource scholarships for college